Однако досрочное погашение сложно оценить, это наиболее сложная задача в моделировании поведения кредитов. Реализация кредитного риска происходит по разным кредитам сходным образом, описывается похожими статистическими методами. Но шаблоны досрочного погашения по разным кредитам сильно отличаются:
• по специализированному финансированию (синдицированное кредитование, проектное финансирование) досрочное погашение, (нарушение контрактного графика, не являющееся кредитным событием), происходит редко и не приветствуется в практике рынка;
• коммерческие кредиты, направленные на обеспечение постоянного финансового рычага для заёмщика, работающего в реальном секторе, обычно привлекаются на длительный срок (например, около 3 лет) и досрочно гасятся, когда появляется возможность рефинансировать эти кредиты на очередной период (обычно за полгода до контрактного погашения); по сути в рамках данной бизнес-модели кредиты являются эшелоном фондирования наряду со средствами акционеров;
• бизнес-модель коммерческого кредитования, направленного на краткосрочное включение финансового рычага (кредиты на оборотные средства для реализации краткосрочных бизнес-идей), вообще не предусматривает, что контрактный график погашения имеет какое-либо значение при отсутствии кредитных событий: когда необходимо приложить усилие, применяется финансовый рычаг, как только необходимость в усилии пропадает, кредит гасится, а кредитная линия переходит в режим ожидания следующих бизнес-возможностей.
Во всех перечисленных вариантах моделирование либо невозможно, либо бесполезно:
• невозможно — потому что данных для этого не хватает, кредитный портфель довольно крупного банка может состоять из десятка кредитов первого типа, нескольких десятков кредитов второго типа и нескольких сотен — третьего типа;
• бесполезно — потому что даже при построении подтверждаемой модели (о принципе подтверждаемости — см. п. 5.5.17 МСФО 9) сохраняются значительные риски отклонения поведения кредита от смоделированного.
Величина обесценения согласно п. B5.5.29 представляет собой разницу приведённых стоимостей контрактных платежей и ожидаемых платежей. Дисконтирование при этом осуществляется по эффективной процентной ставке, и будет логичнее, если все модельные результаты окажутся сконцентрированы в моделировании ожидаемых платежей.
Таким образом, требование об учёте ожидаемого досрочного погашения при расчёте эффективной процентной ставки оказываются практически невыполнимыми и обычно игнорировались. Все эти сложности оказались отражены при переходе от МСФО (IAS) 39 к МСФО (IFRS) 9. В стандарт внесена оговорка, позволяющая «в тех редких случаях, когда надёжная оценка денежных потоков или ожидаемого срока действия финансового инструмента (или группы финансовых инструментов) не представляется возможной, ... использовать данные по предусмотренным договором денежным потокам». Почему эти случаи названы редкими, конечно, вопрос, но практического значения он не имеет.
Когда досрочное погашение можно всё-таки учесть? Это возможно для розничных кредитных портфелей, для которых работает закон больших чисел.
По кредитам с аннуитетными выплатами (то есть таким кредитам, по которым платежи регулярные и одинаковые) график погашения описывается формулой:
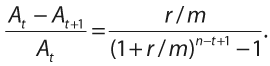
Здесь A — сумма основной части долга, на основе которой начисляются проценты, выплачиваемые по ставке r в момент выплаты t, m — частота выплат по кредиту (обычно 12 раз в год), n — число выплат по кредиту (для двухлетнего кредита — 24). Эффективная процентная ставка YTM определяется из уравнения
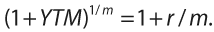
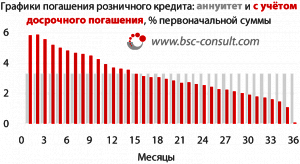
Реальный поведенческий график погашения розничных кредитов может существенно отличаться от контрактного аннуитетного (см. рисунок). Однако опыт показывает, что эффективная процентная ставка от этого зависит слабо: в приведённом примере отличие в восьмом знаке после запятой. Это объяснимо тем, что на эффективную процентную ставку влияет частота выплат основного долга, а их распределение — в гораздо меньшей степени.
Про эффективную ставку и досрочное погашение, вероятно, всё. Более интересный вопрос — как корректный учёт досрочного погашения, обоснованная и подтверждаемая модель, позволяют повысить устойчивость банка и снизить резервы. Но об этом — в другой раз.


